כמה נמוך אפשר לרדת?

אני זוכר פעם בפורום 8 בתפוז, בימיו הטובים לפני 15 שנה, היו דיונים אין סופיים על היגוי הפוך, מדוע האופנוע נוטה הצידה בפניה ומכונית לא, ועוד דיונים תיאורטיים. לאחרונה, ממש במקרה נתקלתי בהרצאה שפרסם לפני כשנתיים פרופסור אלאן רט מאוניברסיטת דרום לואיזיאנה שבארה"ב. רט הוא פרופסור לפיסיקה וגם אופנוען, ובאתר WIRED העלה הרצאה שהכין לסטודנטים שלו לפיסיקה לתואר ראשון ואשר את עיקריה אנחנו מביאים כאן בצירוף הסברים, ציורים וכן, גם משוואות פשוטות להדגמה.
אז קדימה, מתחילים. אחד הכללים הכי פשוטים בפיסיקה שכולנו מכירים הוא שכח משנה את התנועה של גוף מסויים. וניתן לכתוב זאת במשוואה כך:
F הוא הכח m זו המסה של הגוף ו-a התאוצה שלו
כאשר כח פועל על גוף הוא מאיץ בדיוק כמו שתחזיקו כדור ביד ואז תעזבו אותו. מה יקרה? הוא יפול מטה כי הכח הפועל עליו הוא כח המשיכה, כלומר התאוצה תהיה בכיוון שבו הכח פועל.
עכשיו נתאר מצב שבו אתם מאיצים במכונית והצעצוע שתלוי לכם על המראה מתנדנד קדימה ואחורה, מדוע זה קורה? הרי אמרנו שהעצם נע בכיוון הכח המופעל עליו?
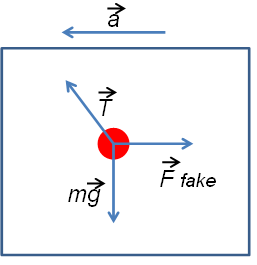
ובכן, הבה נבחן אילו כוחות עובדים על הצעצוע. יש לנו את כח המשיכה כלפי מטה וכח החוט התופס את הצעצוע כלפי מעלה ואת התאוצה קדימה. במצב מנוחה הצעצוע נמצא בשיווי משקל בין כוחות המשיכה והחוט התופס אותו ולכן לא נע כלל, אבל במצב תאוצה האיזון מופר ולכן הוא נע קדימה. אבל מה מניע אותו אחורה?
לשם כך נכניס מושג חדש: הכח המדומה. מכיוון שהמשוואה שנכתבה על ידי ניוטון עובדת רק עבור מערכת שאיננה בתאוצה עלינו להכניס לה תיקון באמצעות הכח המדומה.
הכח המדומה נמצא בכיוון מנוגד לתאוצת המכונית, זהו הכח שבעצם מושך את הצעצוע אחורה במכונית המאיצה קדימה. והוא נכתב כך:
עד היום לא למדתם על על הכח המדומה מכיוון שגם ככה קשה לתלמידים לזהות ולהבין את הכוחות הפועלים והוספה של כח מדומה רק מסבכת את העניינים, לכן תמיד למדו זאת על ידי התבוננות על עצם בתאוצה כאשר הצופה נמצא במצב סטטי, עומד במקום ולא בתוך המערכת המאיצה.
אותו הדבר גם עבור אופנוע בפניה. וקטור המהירות (כלומר הכיוון שלו) של אופנוע משתנה כי יש לו תאוצה למרות שהספידומטר מראה שהמהירות קבועה. זה אומר שהכח המדומה דוחף את האופנוע הפוך לכיוון התאוצה. התאוצה בפניה מושכת לתוך מרכז הסיבוב ומתמטית ניתן לרשום אותה כך:
כאשר r הוא רדיוס הסיבוב, ו-v הוא וקטור המהירות של האופנוע
לכח המדומה הזה אנחנו קוראים הכח הצנטריפוגלי שמשמעו הכח שעוזר לנו לברוח ממרכז הפניה. הכח הצנטריפולי הוא העיקרון המנחה במכשיר הנצטריפוגה שם לדוגמה מבחנה מסתובבת במהירות גבוהה מאוד וכתוצאה ממהירות זו החומר הנמצא בתוך המבחנה שוקע בתחתיתה כי הכח הצנטריפוגלי בעצם מעיף אותו החוצה מהסיבוב. (נא לא לבלבל את הכח הצנטריפוגלי עם הכח הנצטריפטלי אשר גורם לגוף לנוע בסיבוב).
תנע (מומנט)
כאשר מכונית או אופנוע נמצאים בפניה, ישנו כוח נוסף הדוחף אותם בכיוון הפניה וזהו כח החיכוך שנוצר כתוצאה מחיכוך גלגלי האופנוע או המכונית עם הכביש. כח זה חשוב מאוד כאשר נתבונן באופנוע פונה.
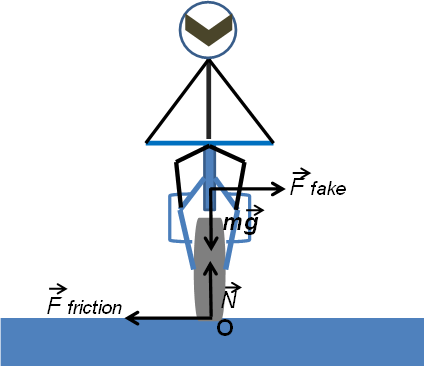
נתבונן על אופנוע הנמצא בפניה ואשר איננו נוטה הצידה אל תוכה. כאשר אופנוע פונה הוא מאיץ אל תוך הפניה ובתגובה הכח המדומה דוחף החוצה. הבה נתבונן בציור:
אנו מסתכלים על אופנוע הפונה ימינה שלו, ולכאורה כל סכום הכוחות שווה לאפס. כח החיכוך מנוגד ושווה לכח המדומה (הצנטריפוגלי) וכח המשיכה (mg) שווה לכח המופעל נגדית מהקרקע. אבל, סכום המומנטים איננו שווה לאפס. לצורך הדגמה נעזוב רגע את האופנוע, תיכף נחזור אליו, וניקח עיפרון, כמו בציור, אם נפעיל על העיפרון כוחות בכיוונים מנוגדים כאשר שניהם באותו מרחק ממרכזו אזי העיפרון ישאר במקומו ולא יזוז אך ברגע שנשנה את מיקום הכוחות זה ביחס לזה או נפעיל רק כח בכיוון אחד הנ"ל יזוז.
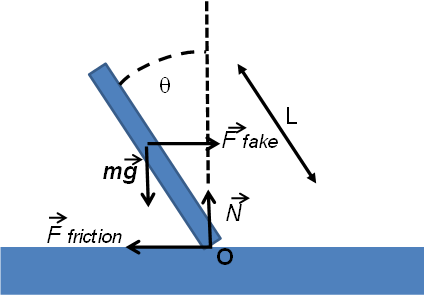
בדיוק כמו שכח משנה מהירות של גוף כך גם המומנט משנה את המהירות הזוויתית. כשהמומנט אפס לא יהיה שינוי במהירות הזוויתית. המומנט תלוי בגודל הכח, במרחק של הכח מנקודת סיבוב מסויימת והזווית שבה הכח מופעל. מתמטית זה נכתב כך:
כאשר q היא הזווית בין הכח F לרדיוס הסיבוב r
נחזור עכשיו לציור של האופנוע הפונה ללא נטייה הצידה, בדיוק כמו בעיפרון, כח החיכוך והכח המדומה לא נמצאים באותו מקום ולכן המומנט הכללי לא שווה אפס והאופנוע ייפול. כאשר האופנוע נוטה הצידה בפניה סכום הכוחות במערכת המאיצה עדיין שווה אפס אבל עתה גם סכום המומנטים שווה אפס ולכן האופנוע אינו נופל.
נסתכל על הציור של האופנוע הנוטה הצידה. המומנט המחושב עבור הנקודה בה גלגל האופנוע נוגע בקרקע שווה אפס מכיוון ששני הכוחות, החיכוך והכח הנורמלי הדוחף מהקרקע מעלה, מופעלים בצורה נגדית בנקודה בה המומנט מחושב. זה משאיר לנו את המומנט הנוצר מהכח המדומה וכח המשיכה וגם כאן מכיוון ששניהם יוצאים מאותה נקודה ומנוגדים זה לזה, הם מבטלים אחד את השני ומתקבל מומנט אפס המונע מהאופנוע ליפול בניגוד למצב של האופנוע הישר שם מומנט המשיכה לא ביטל את המומנט הנוצר מהכח המדומה (צנטריפוגלי, להזכירכם) ולכן האופנוע נופל. המסקנה מכך היא שהטיה של האופנוע בסיבוב מונעת ממנו ליפול.
עכשיו אחרי שהבנו למה האופנוע נוטה הצידה בסיבוב נדבר על כמה נמוך אפשר לרדת בהטיה.
לפני שפשוט נחשב זאת אנו ממליצים לכם לצפות בסרטון הזה של האתר הרשמי של מוטוGP המסביר כיצד הרוכבים לוקחים את הסיבוב ולאיזו זוויות ניתן להגיע:
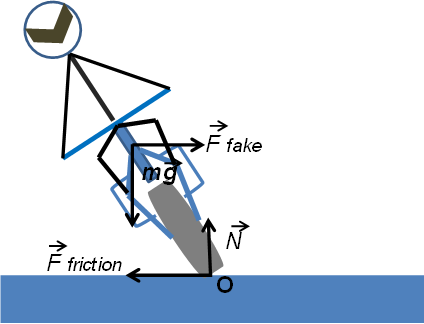
ככל שהפניה הדוקה יותר כך צריך להשכיב את האופנוע יותר. כדי לחשב את זווית הסיבוב נתבונן בציור הבא:
בציור הזה מיקמנו את מרכז המסה היכן שנמצא הכח המדומה, היכן שאנו חושבים שהוא פועל. מכיוון שאנו מחשבים זאת במערכת הנמצאת בתאוצה הכוחות הפועלים יהיו שווים לאפס בשני הכיוונים X (הנע ימינה-שמאלה) ו-Y (הנע מעלה-מטה).
Fy = N-mg = 0
Fx = Ffake-Ffriction = 0
הכח המדומה הוא בעצם הכח הצנטריפוגלי ומכאן נקבל:
עכשיו נכתוב את סכום המומנטים עבור הנקודה O. מכיוון שכח החיכוך והכח הנורמלי עוברים בנקודה O אז מתקבל שהסכום שלהם שווה לאפס.
המשמעות של זה היא שככל שהרוכב מגיע מהר לפניה כך זווית ההטיה תהיה גדולה יותר. כנ"ל גם עבור פניה בעלת רדיוס סיבוב קטן.
אז עד כמה נמוך ניתן לרדת? – זה תלוי בכח החיכוך. אם נחשב את כח החיכוך המקסימלי נדע עד כמה נמוך ניתן לרדת. המודל לחישוב כח חיכוך שבו בדרך כלל משתמשים, עבור צמיג שאינו מחליק, אומר שכח החיכוך פרופורציונאלי לכח הנורמלי, אותו כח נגדי מהקרקע.
עכשיו נציב את זה במשוואה ונקבל:
נציב זאת במשוואת הזווית ונקבל:
כלומר הזווית תקבע על ידי מקדם החיכוך, ולפיכך אם נציב מקדם חיכוך של 0.7 נקבל זווית הטיה של 35 מעלות. אבל אנחנו יודעים שבמוטוGP הרוכבים מגיעים לזווית של 64 מעלות אפילו, ואם נציב זאת במשוואה נקבל מקדם חיכוך של 2.05.
כאן אנחנו לכאורה מקבלים סתירה, כי המודלים שאותם לימדו אותנו בבית הספר ובתואר ראשון אמרו לנו שמקדם החיכוך הוא בין אפס לאחד למרות שלמעשה חיכוך הוא עניין הרבה יותר מסובך ולא בהכרח חייב לציית לכלל הזה.
אז האם לצמיגי אופנועים יש מקדמי חיכוך כאלו גבוהים?
בואו נסתכל על אופנוע בסיבוב וננסה לחשב את התאוצה הזוויתית וממנה את מקדם החיכוך.
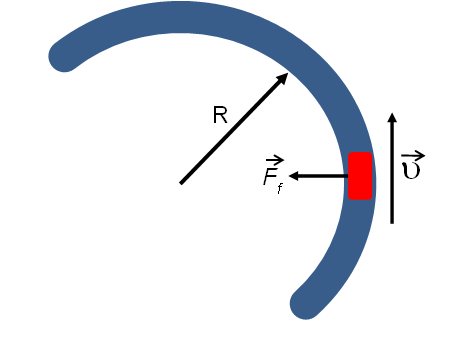
נסתכל על הציור הבא, ממבט על, על אופנוע הנמצא בסיבוב:
בהסתמך על מודל פשוט לחיכוך והביטויים המוכרים לנו על גוף הנמצא בתנועה במעגל נקבל:
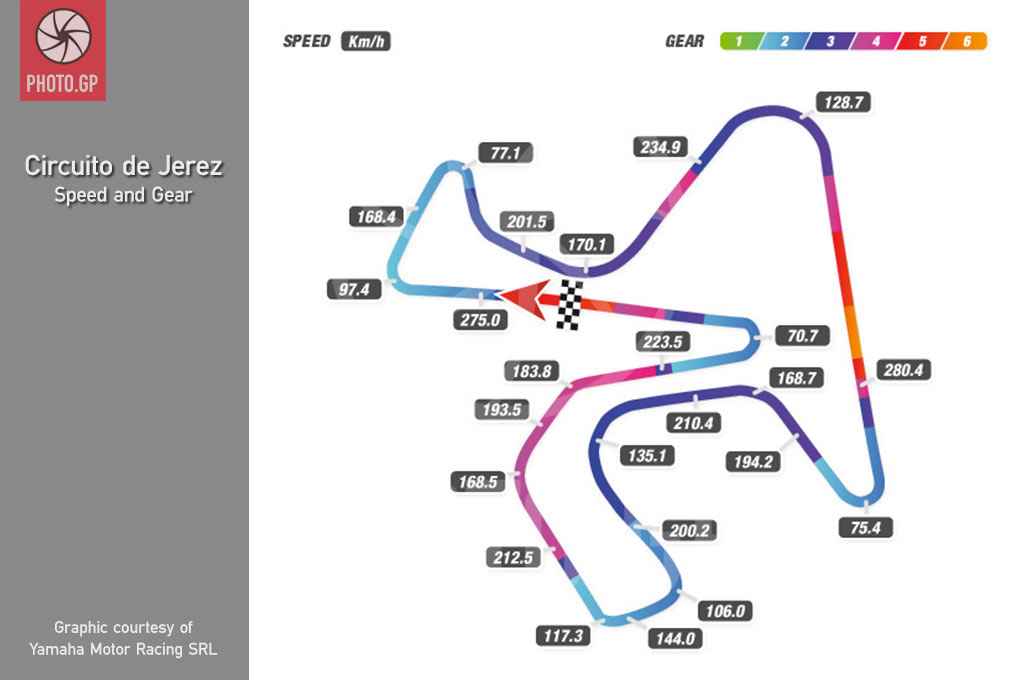
עכשיו נבחר מסלול מוטוGP שעליו נמצא נתונים על מהירות האופנוע בפניה עבור מספר פניות ונחשב את מקדם החיכוך. כאן באתר ניתן למצוא מפות מסלולים עם המהירות הממוצעת באזורים שונים במסלול. אנחנו נתמקד במסלול חרז ונחשב עבור פניות ארבע וחמש שבתמונה.
עבור פניה מספר 4, רדיוס הסיבוב הוא 114.8 מטר, המהירות הנתונה מאתר המוטוGP הרשמי היא 128.7 קמ"ש ולצורך החישוב נמיר אותה למטרים לשניה ונקבל היא 35.6 מטר לשניה, והתאוצה היא 10.98 מטר לשניה בריבוע. אנו מציבים זאת בנוסחה ומקבלים שמקדם החיכוך המינימלי הוא 1.12.
עבור פניה מספר חמש, רדיוס הסיבוב הוא 35.34 מטר, המהירות הנתונה מאתר המוטוGP הרשמי היא 75.4 קמ"ש ולצורך החישוב נמיר אותה למטרים לשניה ונקבל 20.9 מטר לשניה והתאוצה היא 12.41 מטר לשניה בריבוע. מכאן קיבלנו שמקדם החיכוך הוא המינימלי הוא 1.27.
הראינו בדרך אחרת שעדיין אנחנו מקבלים מקדם חיכוך הגבוה מאחד עבור פניה בסיבוב ללא החלקה של הצמיגים, כמו שלורנצו פונה, אז למרות שמקדם חיכוך של 2.05 עבור הצמיגים נראה גבוה ומופרך עדיין אפשר לקבל ערכים הגבוהים מאחד עבור מקדמי חיכוך.
טוב, אז אחרי שהראינו שניתן לקבל מקדם חיכוך גבוה מ-1 בשתי דרכים שונות ובלתי תלויות אנחנו יכולים לחזור אל הנוסחה שבה טנגס הזווית שווה למקדם החיכוך ובמידה ואנו יודעים את מקדם החיכוך של הצמיג מראש אזי נוכל לחשב עד כמה נמוך נוכל לרדת בהטיה.
כל מה שנשאר לעשות הוא לקחת את האופנוע ולנסות זאת במציאות, מישהו מתנדב?

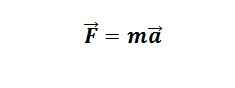
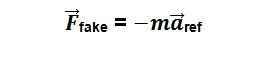
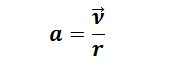

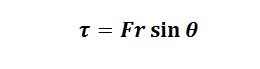
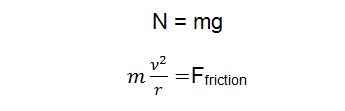
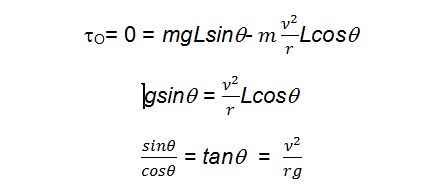
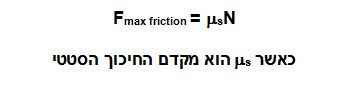
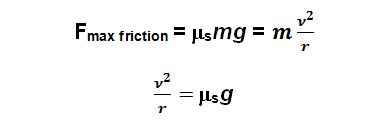
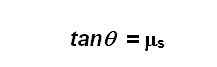
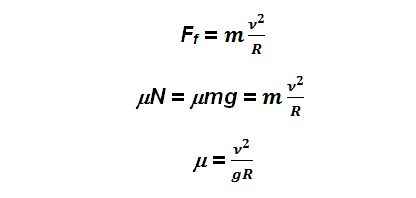

קישור למאמר המקורי בבקשה
קראתי את הרישא בדבריך, אכן היו לפני 15 שנה התפלמסויות הנוגעות במכאניקה הניוטונית.
נעשה פאסט פורווארד להיום –
בפורום בו אני חסום יש דיון סוער עם הכותרת "אבטיפוס לטכנולוגית ייצוב עצמי של הונדה" בו כל המשתתפים מתפלמסים אם בעד או נגד.
https://www.youtube.com/watch?v=VH60-R8MOKo
ואף אחד. אבל אף לא אחד לא חוזר לבייסיק ולמשוואות שנכתבו פה.
אף אחד אפילו לא חשב שעלולה להיות תביעה של גוגל נגד הונדה –
https://www.youtube.com/watch?v=LSZPNwZex9s
(רוצה לומר – פתאים לא מתים)
סליחה על העוף ותודה על ההקשבה.
כמוני כמוך
גם אני פרשתי בשיא אחרי הרישא…
וזה לחלוטין לא אומר שאין לנו בז'רגון מילים כמו קופיצנט, כן?
יש כאן שגיאה, התאוצה היא לא המהירות חלקי הרדיוס אלא ריבוע המהירות חלקי הרדיוס
הרבה זמן חיפשתי סקירה פיסיקלית בנושא, למרות שאני מכיר את רוב הפרטים, כיף לקרוא!
תכלס הנוסחה היא הרבה יותר פשוטה t+b=la
הכל טוב ויפה עד שמגיעים למעבר חציה בישראל
מאמר מקורי
https://www.wired.com/2015/08/motorcycles-lean-far-without-tipping/